
The coefficient of \(n^2\) is half the second difference, which is 1. Worksheets are Nth term practice questions, Finding nth term of a sequence work gcse, Finding the n term question 16, Math 1020 work sequences, Work 3 6 arithmetic and geometric progressions, Introduction to sequences, Quadratic sequences, Arithmetic sequences date period. The sequence will contain \(2n^2\), so use this: \ Displaying all worksheets related to - The Nth Term. SKU: 210 Categories: Algebra, Foundation, GCSE, Geometric and Recurrence, Higher, Interactive Lessons, Patterns and Sequences, Sequences (H), Year 10 Term 1, Year 10 Term 4 Tags: 4 Part Lesson, Ages 14 - 16. The coefficient of \(n^2\) is half the second difference, which is 2. The second difference is the same so the sequence is quadratic and will contain an \(n^2\) term.

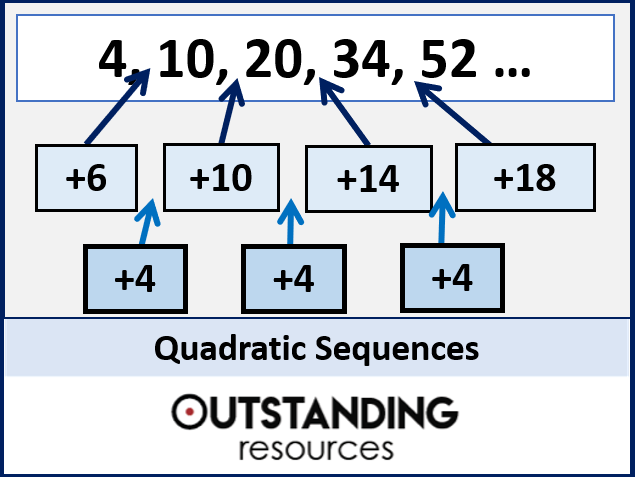
Work out the \(n\) th term of the sequence 5, 11, 21, 35. The \(n\) th term of this sequence is therefore \(n^2 + 1\). GCSE (1 9) Quadratic Sequences Name: Instructions Use black ink or ball-point pen. In this example, you need to add 1 to \(n^2\) to match the sequence. To work out the \(n\) th term of the sequence, write out the numbers in the sequence \(n^2\) and compare this sequence with the sequence in the question. Half of 2 is 1, so the coefficient of \(n^2\) is 1. In this example, the second difference is 2. The coefficient of \(n^2\) is always half of the second difference. The sequence is quadratic and will contain an \(n^2\) term. The first differences are not the same, so work out the second differences. Work out the first differences between the terms. Work out the \(nth\) term of the sequence 2, 5, 10, 17, 26. The first five terms of the sequence: \(n^2 + 3n - 5\) are -1, 5, 13, 23, 35 Finding the nth term of a quadratic Example 1 Sequences Ks3 Displaying all worksheets related to - Sequences Ks3. when \(n = 1\), \(n^2 + 3n - 5 = 1^2 + 3 \times 1 - 5 = 1 + 3 – 5 = -1\) Part 2: Finding the position to term rule of a quadratic sequence.Write the first five terms of the sequence \(n^2 + 3n - 5\). Terms of a quadratic sequence can be worked out in the same way. In fact, whenever the second difference is a constant value it will be a quadratic sequence. The \(n\) th term for a quadratic sequence has a term that contains \(n^2\). This means that it is a quadratic sequence. They can be identified by the fact that the differences between the terms are not equal, but the second differences between terms are equal. Quadratic sequences are sequences that include an \(n^2\) term. Geometric sequences are formed by multiplying or dividing the same number.Finding the nth term of quadratic sequences - Higher The difference between an arithmetic and a geometric sequenceĪrithmetic sequences are formed by adding or subtracting the same number.11 ProjGraphs in the news 1 lesson 1 homework.

Show that the sequence 3, 6, 12, 24, is a geometric sequence, and. graphical representation before looking at simultaneous equations with a quadratic function. This is not always the case as when r is raised to an even power, the solution is always positive. In a (geometric) sequence, the term to term rule is to multiply or divide by the same value. So, substituting that into the formula for the th term will help us to find the value of : 2 × 4 2 + 4 ×.
#Quadratic sequences worksheet ks3 free#
#Quadratic sequences worksheet ks3 how to#


 0 kommentar(er)
0 kommentar(er)
